На рисунке 13 изображен график движения второго автомобиля в системе отсчета, связанной с первым автомобилем. Написать уравнения движений и построить графики в системе отсчета, связанной с землей (начало координат расположить в месте нахождения первого автомобиля в начальный момент времени), если скорость первого автомобиля относительно земли:
а) направлена по оси X и равна 2 м/с;
б) направлена по оси X и равна 6 м/с;
в) направлена в сторону, противоположную оси XY и равна 2 м/с.
Описать картину движения в каждом случае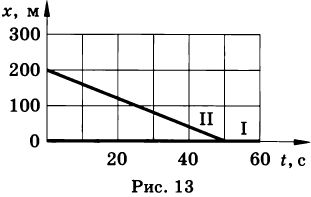
Задача из пособия: Рымкевич А.П. 10-11 класс
Механика
Второе
а) направлена по оси X и равна 2 м/с;
б) направлена по оси X и равна 6 м/с;
в) направлена в сторону, противоположную оси XY и равна 2 м/с.
Описать картину движения в каждом случае
Механика
Решение
Из изображенного в условии задачи графика видно, что начальная координата второго автомобиля (при t=0) x02 = 200 м , а проекция относительной скорости
v ′ 2x 0 − 200 м / 50 с 
v ′ 2 v 2xv 1xv 2 и v 1 - скорости относительно неподвижной системы отсчета, т. е. земли. Из векторного соотношения следует, чтоv ′ 2x v 2x − v 1x
Отсюда, проекция скорости второго автомобиля в системе отсчета, связанной с землей, равна
v 2x = v ′ 2x v 1x
Для первого автомобиля начальная координата x01 = 0 (по условию задачи). Тогда уравнения движения имеют вид:
Для случая а)v 1x = 2 м/с.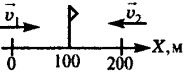 
В случае б)v 1x = 6 м/с.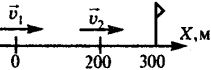 
v 1x > v 2x). Встреча автомобилей произойдет в момент времени tв, определяемый из уравнения:
Первоеx1 = x01 + v 1xt = v1x
x2 = x02 +v 2xt = 200 + (v ′ 2x v 1x) t
x2 = x02 +
Для случая а)
x1 = 2t
x2 = 200 + (−4 + 2) t = 200 − 2t
Машины движутся навстречу друг другу до момента времени tв, определяемого из равенства координат:
x2 = 200 + (−4 + 2) t = 200 − 2t
2tв= 200 - 2tв
tв=200 м / 4 м/с
Далее автомобили будут удаляться друг от друга. tв=
В случае б)
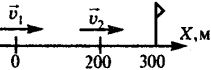
x1 = 6t
x2 = 200 + (−4 + 6) t = 200 + 2t
Сначала первый автомобиль догоняет второй (x2 = 200 + (−4 + 6) t = 200 + 2t
6tв = 200 + 2tв
tв =200 м / 4 м/с
Координата встречи xв = 6 м/с · 50 с = 300 м.tв =
После встречи первый автомобиль удаляется от второго на 20 м за каждую секунду.
В случае в)v 1x = −2 м/с.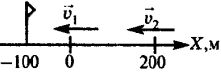 
В случае в)
x1 = −2t
x2 = 200 + (−4 − 2) t = 200 − 6t
Вторая машина догоняет первую. Координата встречи xв = −100 м.x2 = 200 + (−4 − 2) t = 200 − 6t
Второе