Пользуясь графиком проекции скорости (рис. 17), найти начальную скорость, скорости в начале четвертой и в конце шестой секунд. Вычислить ускорение и написать уравнение vx = vx(t).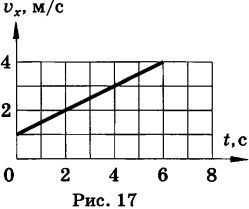 
Задача из пособия: Рымкевич А.П. 10-11 класс
Механика
Второе
Механика
2 способа решения:
1 способ
Из графика следует, что начальная скорость равна 1 м/с, в начале четвертой секунды ее значение 2,5 м/с, а в конце шестой 4 м/с. Ускорение определяется тангенсом угла наклона графика к оси абсцисс и равно 0,5 м/с2. Поэтому уравнение (в единицах СИ) для скорости как функции времени имеет вид
v x(t) = 1 + 0,5t
2 способ
Точка пересечения графика с осью v x показывает нам значение скорости в момент времени t = 0, т. е. v 0x = 1 м/с.
Для определения ускорения возьмем два значения времени: например, t1 = 0 и t2 = 6 c. Им соответствуют значения скоростиv 1 = v 0x = 1 м/с и v 2 = 4 м/с. Воспользуемся формулой
v x = v 0x + axt
Получаем
v x = 1 + 0,5t
ПервоеДля определения ускорения возьмем два значения времени: например, t1 = 0 и t2 = 6 c. Им соответствуют значения скорости
ax = v x − v 0x/ t
Имеем:
ax = v 2 − v 1/ t2 − t1 4 м/с − 1 м/с / 6 с − 0
Подставляем полученные данные в уравнение скорости
Второе