Среднее расстояние между центрами Земли и Луны равно 60 земным радиусам, а масса Луны в 81 раз меньше массы Земли. В какой точке отрезка, соединяющего центры Земли и Луны, тело будет притягиваться ими с одинаковой силой?
Механика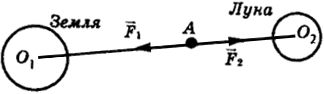
Пусть тело находится в точке A, тогда по условию задачи отрезокO1A = h , а O2A = (60Rз − h) . Отсюда:Mз / h2 Mл / (60Rз − h)2 81Mл / h2 = Mл / (60Rз − h)2 
Задача из пособия: Рымкевич А.П. 10-11 класс
Механика
2 способа решения:
1 способ
Введем обозначения: R - радиус Земли, R1 - расстояние от тела до центра Луны, m1 - масса Луны, m - масса тела. Тогда, согласно условию задачи, расстояние R2 от тела до центра нашей планеты равно 60R − R1 , а масса Земли m2 = 81m1 . Поэтому силы гравитационного взаимодействия тела с Луной и Землей соответственно будут равны:
Решая его, получим:
Fл = G mm1 / R2 1
Fз = Gmm2 / R2 2 81 m1 m / (60R − R1)2
Из равенства этих следует, что справедливо равенство:Fз = G
(60R − R1)2 = 81 R2 1
Решая его, получим:
R1 = 6R
2 способ

Пусть тело находится в точке A, тогда по условию задачи отрезок
F1 = G Mзm / h2
F2 = GMлm / (60Rз − h)2
Когда F1 = F2, то правые части можно приравнять: F2 = G
G Mзm / h2 = G Mлm / (60Rз − h)2
То есть, имеем:h2 = 81 · (60Rз − h)2
Отсюда,h = 9 · (60Rз − h) = 540Rз − 9h
h = 54Rз
Итак, сила притяжения будет иметь одно и то же значение в точке, отстоящей на 54 земных радиуса от центра нашей планеты, или на 6 земных радиусов от центра ее спутника.h = 54Rз
