Определить вес мальчика массой 40 кг в положениях А и В (рис. 30), если R1 = 20 м, v1 = 10 м/с, R2 = 10 м, v2 = 5 м/с. 
Задача из пособия: Рымкевич А.П. 10-11 класс
Механика
Механика
2 способа решения:
1 способ
Случай A.
Расставим силы тяжестиm 
gN 1, сообщающие ребенку центростремительное (нормальное) ускорение a ц (рис. A).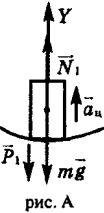 
aц = v 2 1 , получим
P 1 = −N 1
Для модуля силы получим
Случай B.
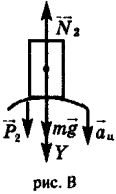
По аналогии с первым случаем, получим проекции на ось Y (рис. B)
Расставим силы тяжести
gNama ц = mg + N 1
В проекции на ось Y имеем: agNN1 − mg = maц
Откуда N1 = m(g + aц)
Учитывая, что центростремительное ускорение имеет формулу N1=m(g + v 2 1
В соответствии с третьим законом Ньютона вес мальчика PNДля модуля силы получим
P1 = N1 = m g + v 2 1 / r1 = 40 кг · 10 м/с2 + (10 м/с)2 / 20 м = 600 Н
Случай B.
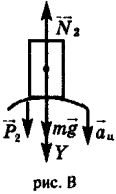
По аналогии с первым случаем, получим проекции на ось Y (рис. B)
mg − N2 = maц = mv 2 2
При этом его вес будет равен P2 = N2 = m g − v 2 2 / r2 = 40 кг · 10 м/с2 − (5 м/с)2 / 10 м = 300 Н
2 способ
В точках A и B уравнение второго закона Ньютона в проекции на вертикальную ось имеет вид
maA,B = N − mg
Ускорение ребенка в точке A направлено вертикально вверх и равно по модулю
aA = v 2 1 / R1
Ускорение в точке B имеет направление вниз и численно равно aB = v 2 2 / R2
Поэтому вес в положениях А и В имеет значение соответственно PA = NA = mg + m v 2 1 / R1
PB = NB = mg −m v 2 2 / R2
Произведем вычисления:
PB = NB = mg −
PA = 40 · 9,8 + 102 / 20 Н = 592 Н
PB = 40 ·9,8 − 52 / 10 Н = 292 Н
PB = 40 ·