По прямолинейной автостраде (рис. 8) движутся равномерно: автобус — вправо со скоростью 20 м/с, легковой

По прямолинейной автостраде (рис. 8) движутся равномерно: автобус — вправо со скоростью 20 м/с, легковой автомобиль — влево со скоростью 15 м/с и мотоциклист — влево со скоростью 10 м/с. Координаты этих экипажей в момент начала наблюдения равны соответственно 500, 200 и -300 м. Написать их уравнения движения.
Найти:
а) координату автобуса через 5 с;
б) координату легкового автомобиля и пройденный путь через 10 с;
в) через какое время координата мотоциклиста будет равна -600 м;
г) в какой момент времени автобус проезжал мимо дерева;
д) где был легковой автомобиль за 20 с до начала наблюдения.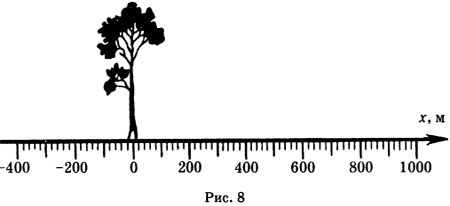

Задача из пособия: Рымкевич А.П. 10-11 класс
Механика

Решение

В соответствии с рисунком к задаче, начало координат совмещено с деревом. Схематично изобразим движение транспорта: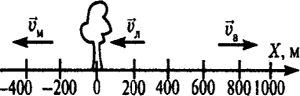

Уравнение прямолинейного равномерного движения имеет вид:

x = x₀ + v_xt

где x₀ - начальная координата тела, v_x — проекция скорости на ось OX. В соответствии с этим запишем уравнения движения каждого вида транспорта:
для автобуса:

x_a = 500 + 20t

для легкового автомобиля:

x_л = 200 − 15t

для мотоциклиста:

x_м= −300 − 10t

а) Чтобы найти координату тела, надо в уравнение движения подставить время. Имеем:

x_a = 500 + 20 · 5 = 600 (м)

б) x_л = 200 − 15 · 10 = 50 (м)
Путь рассчитаем по формуле:

s_л = v_л · t = 15 м/с · 10 с = 150 (м)

в) Чтобы найти время, надо в уравнение движения подставить координату и решить его относительно времени:

x_м = −300 − 10t;

−600 = −300 − 10t

Получаем t = 30 с.

г) Когда автобус проезжал мимо дерева, его координата была равна 0, т.е.

0 = 500 + 20t

Отсюда,

t = 25 с

Знак минус означает, что он проезжал мимо дерева за 25 с до начала наблюдения.

д) В уравнение

x_л = 200 − 15t

надо подставить t = −20 с, т. к. по условию спрашивается, где была машина за 20 с до начала наблюдения. Таким образом, x_л = 200- 15 · (-20) = 500 м

Первое

По прямолинейной автостраде (рис. 8) движутся равномерно: автобус — вправо со скоростью 20 м/с, легковой Рымкевич А.П. 10-11 класс

Второе