Так как упавшая удочка неподвижна относительно воды, рыболову, чтобы ее догнать, нужно столько же времени, сколько прошло после потери, т. е. 1 мин. Поэтому общее время с момента потери составляет 2 мин. Расстояние от места, где рыбак обронил удочку, до места, где он ее догнал, равно произведению времени, прошедшим с момента потери, на скорость течения (ведь удочка покоится относительно воды):

Изобразим схему, предложенную в условии задачи, на чертеже. 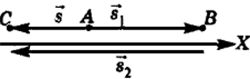Поскольку удочка покоится относительно системы отсчета, связанной с рекой, рыболову потребуется такое же время, т. е. 1 мин, чтобы догнать ее. Пусть в точке A она утеряна, в точке B была обнаружена потеря, а в точке C он догнал ее. Обозначим скорости: v_т - течения , v_л - лодки. Тогда расстояние s₁ от A до B равно: Расстояние от B до C: Длина отрезка пути от A до C: Решим совместно полученные уравнения. s₁ = (v_л − v_т)t
s₂ = (v_л + v_т)t
s = s₂ − s₁ Имеем, s = (v_т + v_л)t − (v_л − v_т)t = 2v_тt = 2 · 2 м/с · 60 с = 240 м