Длина разбега при взлете самолета Ту-154 равна 1215 м, а скорость отрыва от земли 270 км/ч. Длина пробега при посадке этого самолета 710 м, а посадочная скорость 230 км/ч. Сравнить ускорения (по модулю) и время разбега и посадки
Механика

Второе

Задача из пособия: Рымкевич А.П. 10-11 класс
Механика
2 способа решения:
1 способ
Рассмотрим старт самолета. 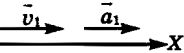
s1x = v 2 1x v 2 01x / 2a1x
v 1x = v 01x + a1xt1
Проекции всех векторов положительные. Отсюда
s1 = v 2 1 / 2a1
v 1 = a1t1Выражаем a1 и t1:
a1 = v 2 1 / 2s1 (1)
t1 =v 1/ a1 (2) Рассмотрим теперь торможение самолета. 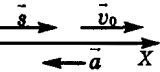
s2x = v 2 2x v 2 02x / 2a2x
v 2x = v 02x + a2xt2Проекция вектора ускорения отрицательна. Откудаs2 = −v 2 02 / −2a2
0 =v 02 − a2t2Выражаем a2 и t2:
a2 = v 2 02 / 2s2 (1′)
t2 =v 02/ a2 (2′) Используя совместно выражения (1) и (1′), (2) и (2′), имеем:
a2 / a1 = v 2 02 / v 2 1 = v 2 02 / v 2 1 (64 м/с)2 · 1215 м / (75 м/с)2 · 710 м t1 / t2 v 1a2/ v 02a175 м/с · 1,25 a1 / 64 м/с · a1
t1 =
0 =
t2 =
a2 = 1,25 a1
t1 = 1,46 t2
2 способ
Для равноускоренного движения (или равнозамедленного (a < 0)) справедливо равенство:
v 2 1 / 2 v 2 0 / 2 = as
При посадке v 1 = 0, s = 710 м, поэтому
v 0= 0, поэтому
v /a, то при посадке t1 = v 0/ a1 v 1/ a2
Произведем вычисления:
Первоеa1 = − v 2 0 / 2s1
При взлете a2 = v 2 1 / 2s2
Так как t = Произведем вычисления:
a1 = (−63,9 м/с)2 / 2 · 710 м
a2 =(75 м/с)2 / 2 · 1215 м
Значит,
a2 =
a1 = 1,25 a2
t1 = 22,2 с; t2 = 32,5. Тогда
t2 = 1,46 t1

Второе
