Написать уравнения x = x(t) для движений, графики скоростей которых даны на рисунке 18. Считать, что в начальный момент (t = 0) тела находятся в начале координат (x = 0).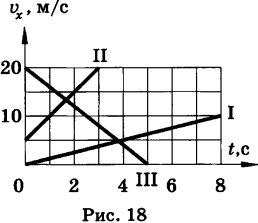 
Задача из пособия: Рымкевич А.П. 10-11 класс
МеханикаПервое
Второе
Механика
Решение
Как известно,
v (t) = v 0 + at (1)
Проанализируем графики, найдем для каждого из них значения ускорения и начальной скорости и подставим их в уравнение движения
x (t) = x0 + v 0t + at2 / 2 (2)
По условию, x0 = 0.
1) Имеем:v (0) = v 0 = 0
v (8) = 10
Поэтому с учетом (1)
2) По аналогии с первым случаем, мы видим, чтоv (0) = v 0 = 5
v (3) = 20
То есть получаем
3) Для третьего графика:v (0) = v 0 = 20
v (5) = 0
Следовательно,
1) Имеем:
10 = a · 8
a = 1,25
Подставляя в (2), получаем результат:
a = 1,25
x(t) = 0,625t2
2) По аналогии с первым случаем, мы видим, что
20 = 5 + a · 3
a = 5
Принимая во внимание (2), имеем:
a = 5
x(t) = 5t + 2,5t2
3) Для третьего графика:
0 = 20 + a · 5
a = −4
Тогда
a = −4
x(t) = 20t − 2t2
Смотрите также:
Второе