Мальчик съехал на санках с горы длиной 40 м за 10 с, а затем проехал по горизонтальному участку еще 20 м до остановки. Найти скорость в конце горы, ускорения на каждом из участков, общее время движения и среднюю скорость на всем пути. Начертить график скорости
Механика

Второе

Задача из пособия: Рымкевич А.П. 10-11 класс
Механика
Решение
Сделаем схематичный рисунок спуска с горки: 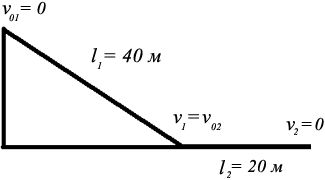
v 01 равна нулю. Тогда, считая движение равноускоренным, запишем:
l 1 = v 01t + a1t2 1 / 2 a1t2 1 / 2 v 1 в конце горы найдем, используя уравнение для скорости при
равноускоренном движении:
v 1 = v 01t + a1t1 = 2l 1 / t1 2 · 40 м / 10 с v 02 = v 1. Учитывая далее, что движение по горизонтальному отрезку пути равнозамедленное до остановки, из уравнения для скорости получим:
v 1 = a2t2 (1)
Путь при равнозамедленном движении
l 2 = v 02t 2 − a2t2 2 / 2 v 1t2 − a2t2 2 / 2 (2)
Решая совместно (1) и (2) относительно a2 и t2, получим
a 2 = v 2 1 / 2l 2 = 2l 2 1 / l 2t2 1 2 · (40 м)2 / 20 м · (10 с)2 v ср = l 1 + l 2/ t1 + t2 60 м / 15 с 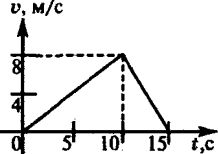
Первое
a1 = 2l 1 / t2 1 = 2 · 40 м / (10 с)2
Скорость 0 = v 1 − a2t2
или
tобщ = t1 + t2 = 10 с + 5 с = 15 с
Средняя путевая скорость по определению:


Второе
