Расстояние между двумя станциями поезд прошел со средней скоростью vcp = 72 км/ч за t = 20 мин. Разгон и торможение вместе длились t1 = 4 мин, а остальное время поезд двигался равномерно. Какой была скорость и поезда при равномерном движении
Механика

Второе

Задача из пособия: Рымкевич А.П. 10-11 класс
Механика
Решение
Задачу целесообразно решать геометрически, построив приблизительный график v x = v x (t) и учитывая, что пройденный путь численно равен площади фигуры, ограниченной графиком и осью абсцисс. 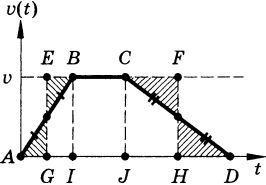
v x (t) представляется графически в виде ломаной линии ABCD. Площадь под ней численно равна всему пути. Проведем вертикальные прямые через точки G и H, соответствующие моментам времени, когда поезд достиг скорости v (t), равной v /2 (половине от максимальной) при его ускорении и торможении. Из рисунка видно, что площадь фигуры ABCD равна площади прямоугольника GEFH. По условию, AI + JD = t1 , AD = t . Так как AG = AI / 2 и HD = JD / 2 , то GH = EF = AD − AG − HD = AD − (AI + JD) / 2 = t − t1 / 2
В то же времяGE = FH = v , поэтому
v ср = s / t v срt = v t − t1 / 2 , откуда
v = v срt/ t − t1/2 v = 2v срt / 2t − t1 v = 72 · 2 · 20 / 2 · 20 − 4
Первое
В то же время
s = SGEFH = GH · GE = v t − t1 / 2
С другой стороны, по определению средняя скорость равна

Второе
